选自《小学数学课程与教学》中《图形与几何-测量》的教学

在小学数学中，圆是第一、二学段学习的平面图形中唯一的一个曲线图形， 是学生第一次正式接触并运用极限的数学思想来解决曲线的长度和面积等问题。同时，可以感知转化、类比、统计、函数、盈亏等数学思想。

转化思想

函数思想

探索2 有一种啤酒瓶的底面直径是7厘米，若要三个啤酒瓶捆扎在一起并用绳子绕4周，打结处用去20cm，问: 1.有几种不同的扎法?请画出示意图。 2.哪种扎法好?为什么? 3.不同扎法的用绳长度相差多少厘米？

探索1 图中由五个同样大小的圆组成，请画一条直线将该图分成面积相等的两个部分。

【案例2】圆的面积的求法

案例描述： 教材将圆等分为了若干份扇形，然后将这些扇形“拼成”了近似的平行四边形或长方形，并且分的份数越多，就越接近平行四边形或长方形。由此推导出圆的面积的公式。

圆的直径、半径、周长、面积的公式 　　直径是半径的2倍 公式：d=2r 　　半径是直径二分之一 公式：r=d÷2 　　圆的周长等于圆周率乘直径 公式：c=πd=2πr 　　圆的面积等于半径乘半径乘圆周率 公式：S=πrr

提问：观察一下，你发现了什么呢？

内容分析

在定性研究和定量研究的过程中，可以将圆的周长与正方形的周长类比，提出猜想，并检验。

案例1的绕线和案例2的以三角形代替扇形都是在做“化曲为直”的转化，转化思想是小学数学曲面图形面积学习的主要思想方法。它可以把学生的思维空间引向更宽更广的层次，形成一个开放的思维空间，为学生今后的发展打下坚实的基础。

1.边长越大，它的周长也越大

2.周长是边长的4倍

猜测: 直径越大，它的周长??

猜测: 周长也可能是直径的若干倍。

感知类比思想

极限思想

3个瓶上缠绕部分的3段弧长之和是一个圆的周长，其余是3个直径的长，计算如下 (3×7+7π)×4+20

左右2个瓶上缠绕部分的2段弧长之和是一个圆的周长，其余是2个直径的长，计算如下 (2×7+7π)×4+20

相差一个直径的4倍：28cm

两种捆扎法解析

画法1

画法2

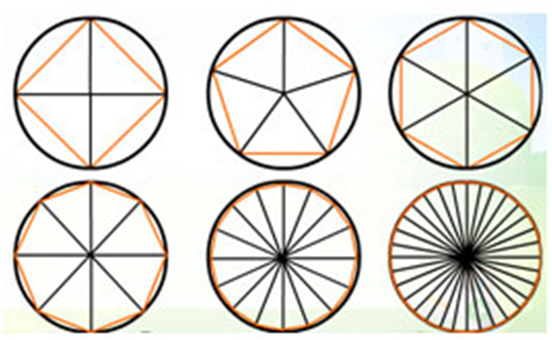
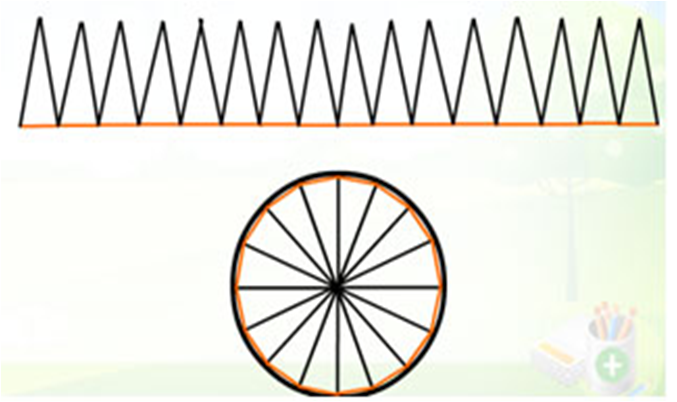
在圆的周长教学中，向学生介绍 “ 割圆术 ” ，让学生经历正多边形到圆的形成过程，引导学生观察体验，随着边数越来越多，正多边形越来越像圆，感受极限思想。

感知极限思想

感知函数思想

盈亏思想

感 知

圆的直径变，周长也变，而且直径越短，周长越短；直径越长，周长越长。圆的周长与它的直径有关系。

同理，圆的直径变，面积也变，而且直径越短，面积越小；直径越长，面积越大。圆的面积与直径有关系。

感知符号化思想

符号化思想

化曲为直： 割之弥补，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣。（刘辉割圆术）

探讨在小学数学教学中渗透数学思想方法，有利于深刻地理解数学的内容和知识体系；有利于提高学生的数学素质；有利于对学生进行美育的渗透和辨证唯物主义的启蒙教育；有利于教师以较高的观点分析处理小学教材。

设计制作：杨 政 奎 制作软件：Focusky

感知转化思想

感知的数学思想

谢谢参观，再见！ 2016.3.11

求圆周率π时，在测量时会产生误差，运用统计的方法可以减少误差。通过统计圆的周长与直径的商的多个值的平均数，从而感知数学统计思想，培养学生实事求是的态度和科学探究的精神。

感知统计思想

统计思想

类比思想

画法3

.

.

.

.

画法5

.

画法4

感知盈亏思想

数学思想在圆的教学中的渗透

Focusky

作品

课

微

Focusky

微

课

作品

杨政奎

感知盈亏思想

练习设计

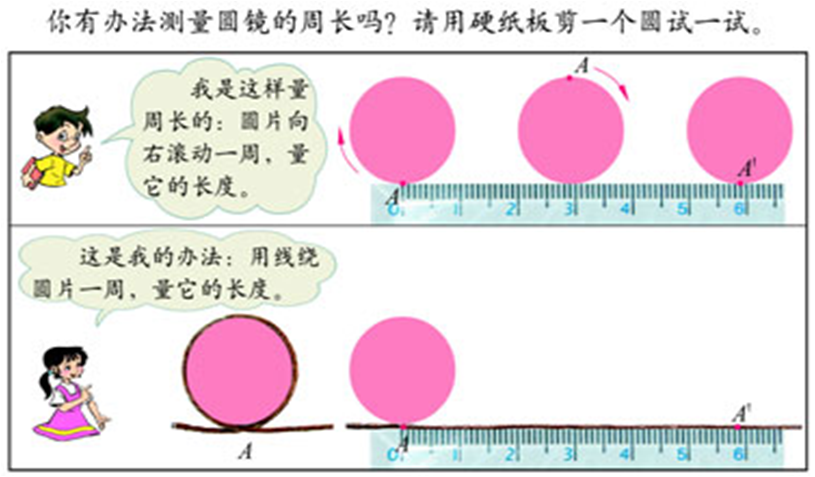
案例 描述 教材采用试一试的方法，用一枚硬币选一个点在直尺上滚动一周，测量圆的周长；另一种是用一条线在硬币上绕一周，测量线的长度。

【案例一】圆的周长公式推导

圆 ——转化——平行四边形、矩形、梯形、三角形

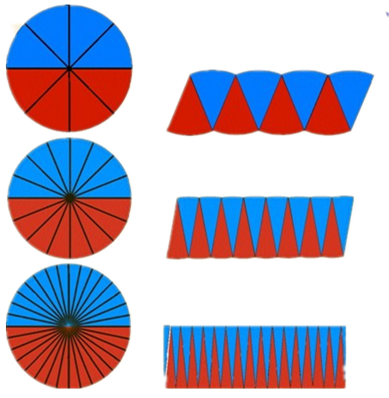
在圆的面积教学中，让学生经历4等分、8等分、16等分、32等分的分割过程，引导学生观察体验，随着所分的等分数越来越大，圆就越来越和平行四边形接近，感受极限思想。